How to derive Linear Equation using Point-Slope Form

So far, we’ve explored linear equations and how they represent lines on a graph. Now, let’s dive into the point slope form, a simple yet powerful method to find the equation of a line when you know its slope and one point on the line. In this guide, we’ll break down the point slope form step-by-step, making it easy to understand and apply. By the end, you’ll be able to confidently derive a linear equation using just a slope and a point!

Recap: What is a linear equation?

In the previous post, we discussed the linear equation in x and y, also named as general equation of a line.

a x + b y + c = 0

where:

• x and y are variables.
• a, b, and c are numbers (called constants).
• The values of a and b cannot both be zero simultaneously, as this would result in the equation no longer being linear.

This form gives us flexibility in describing all types of lines, whether they are sloped or parallel to the axes.

Let’s move onward.

What is Point-Slope Form?

If you know the slope of a line and one point the line passes through, you can easily determine the equation of the line. The formula we use is known as the point-slope form of a linear equation.

The point-slope form is:

y – y₁ = m (x – x₁)

Where:

• m is the slope
• ​ (x₁ ,  y₁) are the coordinates of the given point on the line.

This formula helps us create a linear equation when we know the slope of the line and one point that lies on it. Let’s break it down:

• Imagine the slope is how steep a hill is, and the point is a place where you stand on that hill.
• With the point-slope form, you can figure out what the entire hill (or line) looks like!

Step-by-Step Examples

Example 1:

Problem: Find the equation of the line that passes through the point (1, 3) and has a slope of 2

Step-by-step Solution:

1. Start with the point-slope form:
   • y – y₁ = m (x – x₁)
2. Substitute m = 2, x₁​ = 1, and y₁= 3:
   • y − 3 = 2(x − 1)
3. Simplify the equation:
   • y − 3 = 2x − 2
   • Add 3 to both sides:
     • y – 3 + 3 = 2x – 2 + 3
     • y = 2x + 1
4. So, the linear equation of a line is:
   • y = 2x + 1

Graph:

To plot a graph, it’s easier if we know two points on the line. Since one point is already provided, we can easily determine a second point by putting x = 0. Using the derived linear equation, we can calculate the corresponding y-value, giving us a second point.

The point obtained by setting x = 0 in the equation is called the y-intercept. It represents where the line crosses the y-axis.

With these two points, we can effortlessly draw the line on the graph.

Find another point: Let’s find another point on a line by choosing x = 0.

Put x = 0 in the linear equation we just found.

y = 2x + 1

y = 2(0) + 1 = 1

So, another point is (0,1).

Plot the points (1,3) and (0,1). Connect them to draw the line.

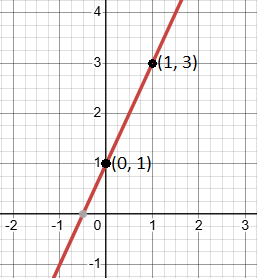
Example 2:

Problem: Find the equation of the line that passes through (2, 1) and has a slope of −1.

Step-by-step Solution:

1. Use the point-slope form:
   • y – y₁ = m (x – x₁)
2. Substitute m = −1, x₁ = 2, and y₁ = 1:
   • y − 1 = -1 (x − 2)
3. Simplify the equation:
   • y − 1 = −x + 2
   • Add 1 to both sides:
     • y – 1 + 1 = −x + 2 + 1
     • y = -x + 3
4. The linear equation of a line is:
   • y = −x + 3

Graph:

Find another point: Let’s find another point on a line by choosing x = 0.

Put x = 0 in the linear equation we just found.

y = -x + 3

y = -(0) + 3 = 3

So, another point is (0,3).

Plot the points (2,1) and (0,3). Connect them to draw the line.

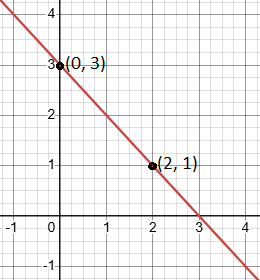
Example 3:

Problem: Find the equation of the line passing through (−2, -1) with a slope of ​.

Step-by-step Solution:

1. Start with the point-slope form:
   • y – y₁ = m (x – x₁)
2. Substitute m = , x₁ = -2, and y₁ = -1:
   • y − (−1) = {x−(−2)}
   • This simplifies to:
     • y + 1 = (x + 2)
3. Distribute the slope:
   • y + 1 = x + (2)
   • y + 1 = x + 3
   • Subtract 1 from both sides:
     • y + 1 – 1 = x + 3 – 1
     • y = x + 2
4. The linear equation of a line is:
   • y = x + 2

Graph:

Find another point: Let’s find another point on a line by choosing x = 0.

Put x = 0 in the linear equation we just found.

y = x + 2

y = (0) + 2 = 2

So, another point is (0,2).

Plot the points (-2, -1) and (0,2). Connect them to draw the line.

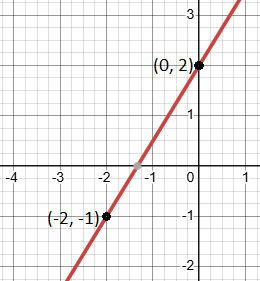
Using Two Points to Draw the Graph

In each example, we’ve been given one point and used it to find the equation of the line. To make drawing the graph easier, we found a second point by selecting any value for x and calculating the corresponding y-value. This method ensures you have two points to connect on the graph, making it simpler to accurately draw the line.

Conclusion

The point-slope form is a great tool to find the equation of a line when you know the slope and a point on the line. By understanding how to use the formula and apply it step by step, you can easily graph and write equations for lines. Practicing with examples like the ones above will help you become confident in using the point-slope form in algebra!

Happy learning!

Related Posts:

1. Introduction. Linear Equation of a line parallel to y-axis
2. Linear Equation and graph of a line parallel to x-axis
3. What is the Slope of a Line
4. How to Calculate the Slope of a Line
5. How to identify and calculate the undefined slope of a line with easy step-by-step solved example.
6. How to Identify Parallel and Perpendicular Lines Using Slopes
7. How to easily find X-Intercept and Y-Intercept of a Linear Equation
8. Slope-Intercept Form of a Linear equation. A Simple Guide