How to Calculate Slope-Intercept Form of a Line

In this guide, we’ll explore how to calculate the slope-intercept form of a line and graph it in different scenarios. The slope-intercept form is one of the most useful ways to write the equation of a line, as it shows the line’s steepness and where it crosses the y-axis. Whether you’re given a slope and y-intercept of a line, two points on the line, a point on a line and parallel to another line or a point on a line and perpendicular to another line, this tutorial will make each step clear with examples and graphs.

By the end, you’ll understand how to calculate the slope-intercept form and use it to easily plot lines on a graph. Let’s get started!

What is the Slope-Intercept Form?

The slope-intercept form of a line is a way to write the equation of a line so that you can easily see the slope and y-intercept:

y = mx + b

• m represents the slope (how steep the line is).
• b is the y-intercept (the point where the line crosses the y-axis).

(For more information, see my post: Slope-Intercept Form of a Linear Equation: A Simple Guide.)

How to Calculate Slope-Intercept Form: Examples and Graphing Steps

Let’s go through four examples to understand how to calculate and graph the slope-intercept form of a line in different cases.

Example 1: Given Slope and Y-Intercept

Problem:

If the slope m = 2 and y-intercept b = −3, find the slope-intercept form of the line and graph it.

Solution:

1. Insert the values of the slope m and y-intercept b into the equation y = mx + b:
   • y = 2x − 3
2. Graphing Steps:
   • Start by plotting the y-intercept point. The y-intercept b being − 3 indicates that it is located at the point (0, − 3).
   • Now, let’s find a second point on the line. The slope of equation y = 2x − 3 is 2​:
     • Since slope is positive, from point (0, – 3), move up 2 units and then right 1 unit to plot the point (1, – 1) on the graph.
   • Draw a line passing through points (0, -3) and (1, – 1) to represent the equation y = 2x − 3.

For a detailed explanation of how to graph the slope-intercept form, including tips and examples, check out How to Graph Slope-Intercept Form.

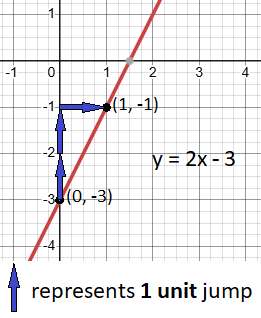
Now, you have graphed the line with a slope of 2 and y-intercept at – 3

Example 2: Given Two Points on the Line

Problem:

Find the equation of a line passing through the points (2, 2) and (1, 3)

Solution:

Formula for Slope

Let and are two distinct points on a non-vertical line. The slope m is given by:

Slope = m =

(If you need a review, check out my post: How to Calculate the Slope of a Line)

1. Calculate the slope m:
   • Slope m = ⇒ = – 1
2. Substitute into the slope-intercept form:
   • y = – x + b
3. Find b:
   • Using point (2, 2), put x = 2 and y = 2 in equation y = – x + b:
     • 2 = – 2 + b
     • Add 2 on both sides
     • b = 4
4. So, the equation of a line passing through the points (2, 2) and (1, 3) is:
   • y = – x + 4
5. Graphing Steps:
   • Start by plotting the points (2, 2) and (1, 3).
   • Draw the line through these points.

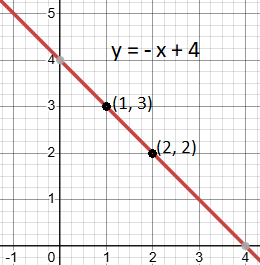
Example 3: Given a Point and a Line Parallel to Another Line

Problem:

Find the equation of a line that passes through (-1, 5) and is parallel to the line y = – 4x + 5.

Solution:

Rule for Identifying Parallel Lines:

Let L₁ and L₂ are two non-vertical lines with slopes m₁ and m₂ respectively. Then the lines L₁ and L₂ are parallel if and only if they have the same slope. That is,

m₁ = m₂ 

(If you need a review, check out my post: How to Identify Parallel and Perpendicular Lines Using Slopes)

1. Since the new line is parallel to the line y = – 4x + 5, so it has the same slope as y = – 4x + 5.
   • Slope of the line y = – 4x + 5 is – 4, so slope m of the new line is also – 4.
2. Substitute the slope m into the equation y = mx + b:
   • y = − 4x + b
3. Find b:
   • (-1, 5) is a point on a new line. Substitute (x, y) = (-1, 5) in y = – 4x + b:
     • y = – 4x + b.
     • 5 = − 4(– 1) + b
     • 5 = 4 + b
     • Subtract 4 on both sides
     • 4 + b – 4 = 5 – 4
     • b = 1
4. The equation of a line that passes through (-1, 5) and is parallel to the line y = – 4x + 5 is:
   • y = − 4x + 1
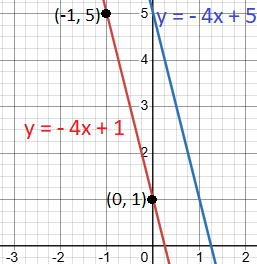
5. Graphing Steps:
   • Plot the given point (-1, 5)
   • The y-intercept being 1 indicates that it is located at the point (0, 1).
   • Draw a line through these two points.

Example 4: Given a Point and a Line Perpendicular to Another Line

Problem:

Find the equation of a line passing through (1, − 2) and perpendicular to the line y = x + 2.

Solution:

Rule for Identifying Perpendicular Lines:

Let L₁ and L₂ are two non-vertical lines with slopes m₁ and m₂ respectively. Then the lines L₁ and L₂ are perpendicular to each other if and only if the product of their slopes is -1. That is,

m₁  m₂  = -1

(If you need a review, check out my post: How to Identify Parallel and Perpendicular Lines Using Slopes)

1. Find the perpendicular slope. Slope of line y = x + 2 is ​. Slope m of a line perpendicular to it would be − 2.
2. Substitute into the slope-intercept form y = mx + b:
   • y = − 2x + b
3. Find b:
   • Substitute (x, y) = (1, − 2) in y = − 2x + b:
     • − 2 = − 2 (1) + b
     • – 2 = – 2 + b
     • b = 0
4. The equation of a line passing through (1, − 2) and perpendicular to the line y = x + 2 is:
   • y = − 2x
5. Graphing Steps:
   • Plot the given point (1, – 2)
   • The y-intercept being 0 indicates that it is located at the point (0, 0).
   • Draw a line through these points.

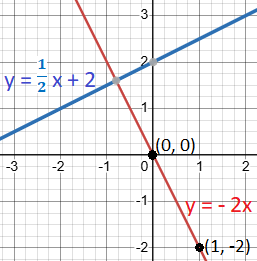
Conclusion

Calculating the slope-intercept form of a line can be done with just a few easy steps, depending on the information you’re given. By following the examples above, you can now confidently determine the slope-intercept form and graph it, whether you know the slope and intercept, need to work from two points or have a point on a line that is parallel or perpendicular to another line.

These examples give you the skills to solve and graph linear equations across different scenarios.

Related Posts:

1. Introduction. Linear Equation of a line parallel to y-axis
2. Linear Equation and graph of a line parallel to x-axis
3. What is the Slope of a Line
4. How to Calculate the Slope of a Line
5. Solved example of finding slope of a line that passes through two given points
6. How to Identify Parallel and Perpendicular Lines Using Slopes
7. How to derive Linear Equation using Point-Slope Form
8. How to easily find X-Intercept and Y-Intercept of a Linear Equation
9. Slope-Intercept Form of a Linear equation. A Simple Guide