How to easily find X-Intercept and Y-Intercept of a Linear Equation

Linear equations are a fundamental part of algebra, and understanding x-intercept and y-intercept helps us analyze and draw lines on a graph. Today, we’ll learn how to find the x-intercept and y-intercept of a linear equation and also explore the intercepts of horizontal and vertical lines. This guide is designed to be simple and beginner-friendly.

What are X-Intercept and Y-Intercept?

• X-Intercept: The point where a line crosses the x-axis. At this point, the y-coordinate is always zero, meaning the value of y is 0 at this point.
• Y-Intercept: The point where a line crosses the y-axis. At this point, the x-coordinate is always zero, meaning the value of x is 0 at this point.

How to Find the X-Intercept and Y-Intercept

For a linear equation in the general form ax + by = c, we can find the intercepts using simple steps:

• To find the x-intercept, set y = 0 and solve for x.
• To find the y-intercept, set x = 0 and solve for y.

Step-by-Step Examples of Finding Intercepts for a Linear Equation

Example 1:

Find Intercepts for 2x + 3y = 6

Step 1: Find the y-intercept

• Set x = 0
• Plug x = 0 into the equation 2x + 3y = 6:
  • 2(0) + 3y = 6
    • 3y = 6
    • y = 2.
• So, the y-intercept is (0, 2)

Step 2: Find the x-intercept

• Set y = 0
• Plug y = 0 into the equation 2x + 3y = 6:
  • 2x + 3(0) = 6
  • 2x = 6
  • x = 3
• So, the x-intercept is (3, 0)

Graph:

• Plot the points (3, 0) and (0, 2) on the graph.
• Draw a line through these points.

This is the graph of equation 2x + 3y = 6

Example 2:

Now, let’s try another example: x − 4y = 4

Step 1: Find the y-intercept

• Set x = 0
• Plug x = 0 into the equation x − 4y = 4:
  • 0 − 4y = 4
  • −4y = 4
  • y =
  • y = – 1
• So, the y-intercept is (0, − 1)

Step 2: Find the x-intercept

• Set y = 0
• Plug y = 0 into the equation x − 4y = 4:
  • x − 4(0) = 4
  • x = 4
• So, the x-intercept is (4, 0)

Graph:

• Plot the points (4,0) and (0, −1) on the graph.
• Draw a line through these points.

This is the graph of equation x – 4y = 4

Example 3:

Let’s find the intercepts for a more challenging equation: 5x – 4y = 10

Step 1: Find the y-intercept

• Set x = 0
• Plug x = 0 into the equation 5x − 4y = 10:
  • 5(0) −4y = 10
  • – 4y = 10
  • y =
  • y = – 2.5
• So, the y-intercept is (0, −2.5)

Step 2: Find the x-intercept

• Set y = 0
• Plug y = 0 into the equation 5x − 4y = 10:
  • 5x − 4(0) = 10
  • 5x = 10
  • x =
  • x = 2
• So, the x-intercept is (2, 0)

Graph:

• Plot the points (2,0) and (0, −2.5)
• Draw a line through these points.

This is the graph of equation 5x – 4y = 10

X-Intercept and Y-Intercept of Horizontal and Vertical Lines

1. Horizontal Line: A horizontal line has an equation like y = k (where k is a constant).
   • X-Intercept: A horizontal line may not have an x-intercept if it’s not on the x-axis.
   • Y-Intercept: The y-intercept is always (0, k).
2. Vertical Line: A vertical line has an equation like x = k (where k is a constant).

Example 4: Horizontal Line y = -2

1. X-Intercept: A horizontal line does not cross the x-axis, so it has no x-intercept.
2. Y-Intercept: The y-intercept is (0, – 2)

Graph: Draw a horizontal line through y = – 2, showing it never crosses the x-axis.

Example 5: Vertical Line x = 1

1. X-Intercept: The x-intercept is (1, 0)
2. Y-Intercept: A vertical line does not cross the y-axis unless it’s the line x = 0

Graph: Draw a vertical line through x = 1, showing it never crosses the y-axis.

Special Cases: X-Intercept and Y-Intercept for x = 0 and y = 0

• Linear Equation x = 0: This represents the y-axis itself. The line coincides with the y-axis, so it does not have an x-intercept, but the entire y-axis is the graph. The y-intercept is every point on the y-axis.

• Linear Equation y = 0: This represents the x-axis. The entire line is the x-axis itself, so the y-intercept does not exist, but every point on the x-axis is the x-intercept.

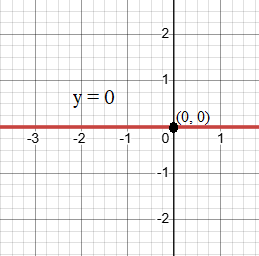
Recap

• The x-intercept is where the line crosses the x-axis.
  • To find it, set y = 0 and solve for x.
• The y-intercept is where the line crosses the y-axis.
  • To find it, set x = 0 and solve for y.
• For horizontal lines (equation y = k):
  • No x-intercept (unless y = 0).
  • Y-intercept is always (0, k)
• For vertical lines (equation x = k):
  • x-intercept is always (k, 0).
  • No y-intercept (unless x = 0).
• For the equation x = 0 (y-axis):
  • No x-intercept but the entire y-axis is the graph.
• For the equation y = 0 (x-axis):
  • No y-intercept but the entire x-axis is the graph.

By following these points, you’ll easily find the intercepts for any linear equation!

Why Are X-Intercept and Y-Intercept Important?

Finding the x-intercept and y-intercept helps us graph linear equations quickly and accurately. They give us two points on the line, and since a straight line can be drawn using any two points, these intercepts make graphing easy. Plus, they help in understanding how the line behaves relative to the axes.

Conclusion

In this guide, we learned how to find the x-intercept and y-intercept of a linear equation. Understanding intercepts is crucial for mastering linear equations and their graphs.

By practicing these steps, you’ll be able to find the x-intercept and y-intercept of any linear equation with ease!

Related Posts:

1. Introduction. Linear Equation of a line parallel to y-axis
2. Linear Equation and graph of a line parallel to x-axis
3. What is the Slope of a Line
4. How to Calculate the Slope of a Line
5. How to identify and calculate the undefined slope of a line with easy step-by-step solved example.
6. How to Identify Parallel and Perpendicular Lines Using Slopes
7. How to derive Linear Equation using Point-Slope Form
8. Slope-Intercept Form of a Linear equation. A Simple Guide