Parallel and Perpendicular Lines: Identify them with Slopes

In algebra, understanding parallel and perpendicular lines is key to mastering graphs and equations. You can easily identify these types of lines by using their slopes. Slopes tell us how steep a line is, and whether two lines are traveling in the same direction (parallel) or intersecting at a right angle (perpendicular).

In this guide, we’ll learn how to identify parallel and perpendicular lines using slopes step-by-step. By the end, you’ll be able to recognize these lines quickly on a graph. Let’s dive into it!

What Are Parallel Lines?

Parallel lines are lines that never meet, no matter how long you extend them. Think of two train tracks—no matter how far they go, they stay the same distance apart and never cross.

Rule for Identifying Parallel Lines:

Let L₁ and L₂ are two non-vertical lines with slopes m₁ and m₂ respectively. Then the lines L₁ and L₂ are parallel if and only if they have the same slope. That is,

m₁ = m₂

Step-by-Step Example 1: Identifying Parallel Lines

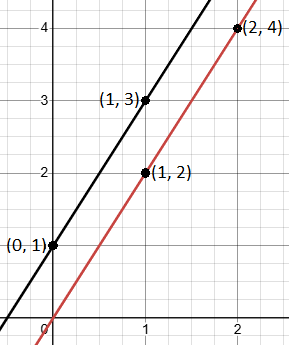
Problem: We have a line passing through points (1, 2) and (2, 4), and another line passes through points (0, 1) and (1, 3). Are these lines parallel?

Find the slope of Line 1 (through points (1, 2) and (2, 4)):
- slope of Line 1 = m₁ = $\frac{y_2-y_1}{x_2-x_1}=\;\frac{4-2}{2-1}=\frac21=2$
Find the slope of Line 2 (through points (0, 1) and (1, 3)):
- slope of Line 2 = m₂ = $\frac{y_2-y_1}{x_2-x_1}=\;\frac{3-1}{1-0}=\frac21=2$
Both lines have the same slope of 2, so they are parallel lines.
Graph:
- Plot points (1,2), (2, 4), (0,1) and (1, 3) on a graph. Construct a line passing through the points (1,2) and (2,4). Then, draw a second line through the points (0,1) and (1,3).
- You will see that these parallel lines never meet, as they move in the same direction.

Learn how to identify parallel and perpendicular lines using slopes. Easy-to-follow examples with graphs included

What Are Perpendicular Lines?

Perpendicular lines intersect at a 90-degree angle, like the corners of a square or rectangle. These lines meet at a right angle, forming an “L” shape.

Rule for Identifying Perpendicular Lines:

Let L₁ and L₂ are two non-vertical lines with slopes m₁ and m₂ respectively. Then the lines L₁ and L₂ are perpendicular to each other if and only if the product of their slopes is -1. That is,

m₁ m₂ = -1

Step-by-Step Example 2: Identifying Perpendicular Lines

Problem: We have two lines. One passes through points (0, 1) and (1, -1), and another passes through points (0, -1) and (1, 1). Are these lines perpendicular?

Find the slope of Line 1 (through points (0, 1) and (1, -1)):
- slope of Line 1 = m₁ = $\frac{y_2-y_1}{x_2-x_1}=\;\frac{-1-1}{1-0}=\frac{-2}1=-2$
Find the slope of Line 2 (through points (0, -1) and (1, 1)):
- slope of Line 2 = m₂ = $\frac{y_2-y_1}{x_2-x_1}=\;\frac{1-(-1)}{1-0}=\frac21=2$
Check the product of their slopes: The slope of Line 1 is -2, and the slope of Line 2 is 2.
- m₁ m₂ = (-2) 2 = – 4 ≠ -1
- So these lines are not perpendicular to each other.
Graph:
- Plot points (0, 1), (1, -1), (0, -1) and (1, 1) on a graph. Construct a line passing through the points (0, 1) and (1, -1). Then, draw a second line through the points (0, -1) and (1, 1).
- You will see that these lines are not perpendicular to each other.

Step-by-Step Example 3: Identifying Perpendicular Lines

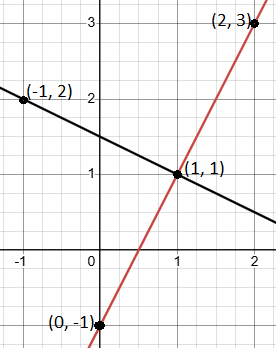
Problem: Let’s check if two lines passing through points (-1, 2) and (1, 1), and points (0, -1) and (2, 3) are perpendicular.

Find the slope of Line 1 (through points (-1, 2) and (1, 1)):
- slope of Line 1 = m₁ = $\frac{y_2-y_1}{x_2-x_1}=\;\frac{1-2}{1-(-1)}=\frac{-1}2$
Find the slope of Line 2 (through points(0, -1) and (2, 3)):
- slope of Line 2 = m₂ = $\frac{y_2-y_1}{x_2-x_1}=\;\frac{3-(-1)}{2-0}=\frac42=2$
Check the product of their slopes: The slope of Line 1 is , and the slope of Line 2 is 2.
- m₁ m₂ = $\left(\frac{-1}2\right)\;\;\left(2\right)$ = -1
- So the lines are perpendicular to each other.
Graph: Plot points (-1, 2), (1, 1), (0, -1) and (2, 3) on a graph, then draw the lines. You’ll see that the lines meet at a right angle, confirming they are perpendicular lines.

Conclusion

Using slopes, it’s easy to identify parallel and perpendicular lines.

Parallel lines have the same slope, which means they run side by side without ever crossing.
Perpendicular lines slopes product is -1, meaning they intersect at a right angle.

Understanding these relationships helps in graphing and interpreting linear equations. By knowing the slopes of lines, you can quickly figure out whether they are parallel or perpendicular and solve problems more efficiently!

How to Identify Parallel and Perpendicular Lines Using Slopes