What are Prime Factors? Simple Steps to Find Them

Prime factors are the building blocks of numbers! They are the prime numbers that multiply together to make a bigger number. But what exactly does this mean? Let’s dive into it step-by-step and learn how to find prime factors.

What Are Prime Factors?

Prime factors are the factors of a number that are prime numbers. A prime number is a number that can only be divided by 1 and itself, without leaving any remainder. Some examples of prime numbers are 2, 3, 5, 7, 11, 13, 17, and so on.

When we break down a number into its prime factors, we are finding which prime numbers multiply together to give the original number.

For example:

Prime factors of 12 are 2, 2, and 3 because 2 × 2 × 3 = 12.
Prime factors of 18 are 2, 3, and 3 because 2 × 3 × 3 = 18.

What is Prime Factorization?

Prime factorization is the process of expressing a whole number as a product of its prime factors.

How to Find Prime Factors

There are two common methods of prime factorization. Let’s understand each method with the help of examples.

METHOD 1: Division Method

Divide by the smallest prime number: Start by dividing your number by the smallest prime number, which is 2.

If the number is divisible by 2 (even), write 2 down as a factor and divide the number by 2.
If the number isn’t divisible by 2, move to the next prime number, which is 3.

Continue with prime numbers: Keep dividing the result by the next smallest prime number until you can’t divide anymore.Let’s try this with a few examples.

Example 1: Prime Factors of 20

Step 1: Start with 20. Divide it by 2 (smallest prime number).
20 ÷ 2 = 10
Step 2: Divide 10 by 2 again.
10 ÷ 2 = 5
Step 3: 5 is a prime number, so we’re done!
Prime factors of 20 are 2, 2, and 5.

We can confirm our answer by multiplying the prime factors together to obtain the original number.

Here, 2 × 2 × 5 = 20. Thus, the prime factors we have found are correct.

Example 2: Prime Factors of 45

Step 1: Start with 45. Divide it by 3 (since 2 doesn’t work).
45 ÷ 3 = 15
Step 2: Divide 15 by 3 again.
15 ÷ 3 = 5
Step 3: 5 is a prime number, so we’re done!
Prime factors of 45 are 3, 3, and 5.

Example 3: Prime Factors of 100

Step 1: Start with 100. Divide it by 2.
100 ÷ 2 = 50
Step 2: Divide 50 by 2 again.
50 ÷ 2 = 25
Step 3: Now, divide 25 by 5 (since 2 no longer works).
25 ÷ 5 = 5
Step 4: 5 is a prime number, so we’re done!
Prime factors of 100 are 2, 2, 5, and 5.

Example 4: Express 990 as a product of its prime factors

Step 1: Divide by the smallest prime number
Start dividing the given number by the smallest prime number, which is 2. Since 2 is a prime number and divides 990 completely, we write down 2 as one of the prime factors.

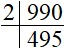
How to Find Prime Factors of a number by division method.

Step 2: Divide the quotient by the next smallest prime number
Now take the quotient (495) and divide it by the next smallest prime number. Here, 3 is the next prime number that divides 495 completely.

Step 3: Continue until you reach 1
Keep repeating this process, dividing the quotient by prime numbers until the quotient becomes 1. Here’s how it goes:

The prime factors of 990 are 2, 3, 3, 5, and 11. Therefore, we can express 990 as:

990 = 2 × 3 × 3 × 5 × 11

METHOD 2: Factor Tree Method

Example 5: Express 990 as a product of its prime factors

Step 1: Find two factors of the number
Begin by finding two numbers whose product equals 990. Let’s pick 99 and 10 because 990 = 99 × 10

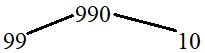
How to Find Prime Factors of a number by Factor-tree method.

Step 2: Break down each factor into smaller factors
Now break down both 99 and 10 into smaller factors. Start with 99:

99 = 3 × 33

Then break down 10:

10 = 2 × 5

Step 3: Repeat until all factors are prime
Keep breaking down the factors until only prime numbers remain at the bottom of your factor tree. The factor tree for 990 looks like this:

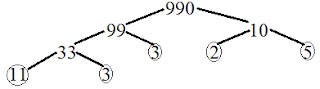
990 = 2 × 3 × 3 × 5 × 11

Both methods give us the same result, with the prime factorization of 990 being:

990 = 2 × 3 × 3 × 5 × 11

Key Takeaway:

The Fundamental Theorem of Arithmetic states that every positive integer has a unique prime factorization. This means no matter how you approach the factorization process, the result will always be the same prime factors, just in a different order.

By using either the division method or the factor tree method, you can easily find the prime factors of any number.

Difference Between Factors and Prime Factors

It’s important to note that factors of a number are all the numbers that can divide it evenly. But prime factors are only the prime numbers that multiply together to make the number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. But the prime factors of 12 are just 2 and 3.

Why Are Prime Factors Important?

Prime factors are important because they help us understand the basic building blocks of numbers. Prime factorization is used in many areas of mathematics, including finding the greatest common divisor (GCD) and least common multiple (LCM) of two numbers. It’s also helpful in cryptography, which is used to keep data secure.

Recap

Remember, prime factors are just the prime numbers that multiply together to give the original number. Mastering this skill will help you with various math problems, from simplifying fractions to advanced number theory.

Now that you know how to find prime factors, try practicing with some more numbers and see how quickly you can break them down!

What are Prime Factors? How to Find Them Easily