Slope-Intercept Form of a Linear Equation. A Simple Guide

In this guide, we’ll explore the slope-intercept form of a linear equation, a key concept in algebra that helps you understand how lines behave on a graph. Whether you’re trying to find the equation of a line or graph it, this form makes things easy to follow. By the end, you’ll know how to find the equation of a line using its slope and y-intercept, and how to interpret it for graphing.

What is the Slope-Intercept Form?

The slope-intercept form of a linear equation is written as:

y = mx + b

Where:

• m is the slope (how steep the line is).
• b is the y-intercept (where the line crosses the y-axis).
• x and y are variables representing points on the line.

This form gives us a simple way to understand the behavior of the line, including how steep it is and where it crosses the y-axis.

Example 1: Finding the Equation of a Line from its Slope and Y-Intercept

Let’s say you are given:

• Slope (m) = 2
• Y-intercept (b) = -1

To write the equation of the line, we just plug these values into the formula y = mx + b:

y = 2x − 1

This is the slope-intercept form of a linear equation for a line with a slope of 2 and a y-intercept of -1.

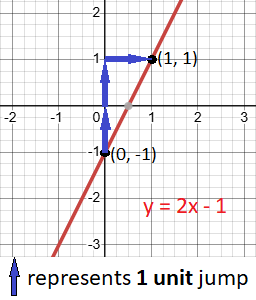
Graphing the Line

1. Start by plotting the y-intercept (0, -1) on the y-axis.
2. Use the slope (m = 2) to find another point:
   • Since slope is positive, so from point (0, -1), move 2 units up and then 1 unit right. This gives the point (1, 1).
3. Connect the points (0, -1) and (1, 1) with a straight line.

For a detailed explanation of how to graph the slope-intercept form, including tips and examples, check out How to Graph Slope-Intercept Form

Example 2: Finding the Slope and Y-Intercept from an Equation

Suppose you’re given the equation: y = −3x + 4

To find the slope and y-intercept, compare y = −3x + 4 with y = mx + b:

• In y = −3x + 4, – 3 is with x so slope (m) is – 3.
• The y-intercept (b) is 4.

This tells us the line is steep and slopes downward, crossing the y-axis at (0, 4).

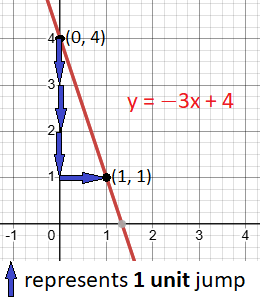
Graphing the Line

1. Plot the y-intercept (0, 4) on the graph.
2. Use the slope (m = – 3) to find another point:
   • As slope is negative, from point (0, 4), move 3 units down and then 1 unit right. This gives the point (1, 1).
3. Connect the points (0, 4) and (1, 1) with a straight line.

Want to learn more about graphing lines step-by-step? Check out this guide on graphing slope-intercept form.

Example 3: Finding the Equation from Two Points

Let’s say you are given two points: (1, 2) and (2, 5). How do we find the slope-intercept form of a linear equation?

1. Find the slope (m):
   • Formula for the slope: If and are two distinct points on a non-vertical line. The slope (m) is given by:
     • Slope (m) =
   • Let = (1, 2) means = 1 and = 2
   • Let = (2, 5) means = 2 and = 5
   • Slope (m) = ⇒ = ⇒ 3
2. Use the slope and one point to find the y-intercept (b): Now, using the slope (m) = 3 and the point (1, 2), we’ll plug them into the formula y = mx + b:
   • 2 = 3(1) + b
   • b = 2 – 3 ⇒ -1
3. Put value of slope (m) and y-intercept (b) in formula y = mx + b:
   • So, the equation of a line passing through two points (1, 2) and (2, 5) is y = 3x − 1

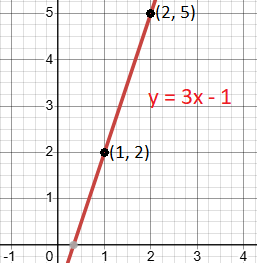
Graphing the Line

1. Plot the points (1, 2) and (2, 5)
2. Connect the points with a straight line.

Conclusion

In this tutorial, you’ve learned about the slope intercept form of a linear equation. We explored how to find the equation from the slope and y-intercept, how to derive the slope and y-intercept from an equation, and how to find the equation from two points. Understanding this form not only makes it easier to write equations for lines but also to graph them effectively.

The slope intercept form provides a clear picture of how a line behaves, allowing you to quickly graph it and analyze its properties. With practice, you’ll find it an invaluable tool in your algebra toolkit!

Related Posts:

1. Introduction. Linear Equation of a line parallel to y-axis
2. Linear Equation and graph of a line parallel to x-axis
3. What is the Slope of a Line
4. How to Calculate the Slope of a Line
5. How to identify and calculate the undefined slope of a line with easy step-by-step solved example.
6. How to Identify Parallel and Perpendicular Lines Using Slopes
7. How to derive Linear Equation using Point-Slope Form
8. How to easily find X-Intercept and Y-Intercept of a Linear Equation