Linear equations play a key role in algebra, and understanding how to express them in different forms is essential for solving various types of problems. In this guide, we will learn about the three main forms of linear equations, their differences, and how to use them. We will also cover the general and standard forms of linear equations, explaining their usage and key differences.
The three main forms of linear equations are:
- Slope-Intercept Form: y = mx + b
- Point-Slope Form: y − y1 = m (x − x1)
- Standard Form: Ax + By = C
Now, let’s dive into each form with explanations and examples, step by step!
1. Slope-Intercept Form: y = mx + b
This is the most common and user-friendly form when graphing linear equations, especially if you know the slope and y-intercept.
- m represents the slope of the line (how steep it is).
- b represents the y-intercept (where the line crosses the y-axis).
Example:
Let’s say the equation is y = 2x + 3.
By comparing the equation y = 2x + 3 with y = mx + b, we find that:
- The slope (m) is 2. This means for every step you take to the right (positive direction on the x-axis), you go up 2 steps.
- The y-intercept (b) is 3. This means the line crosses the y-axis at (0, 3).
Graph:
- Start by plotting the y-intercept at (0,3) on the graph.
- Use the slope (m = 2) to find another point:
- Since slope is positive, from point (0, 3), move 2 units up and then 1 unit right. This gives the point (1, 5).
- Connect the points (0, 3) and (1, 5) with a straight line.
For a detailed explanation of how to graph the slope-intercept form, including tips and examples, check out How to Graph Slope-Intercept Form.
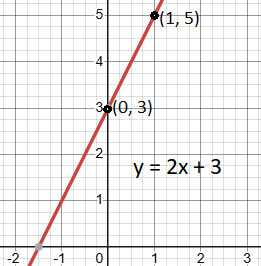
2. Point-Slope Form: y − y1 = m(x − x1)
This form is useful when you know one point on the line and the slope. It helps you create the equation when the y-intercept isn’t given.
- m represents the slope of the line.
- (x1 , y1) is the point on the line.
Example 2:
The slope (m) of a line is 3 and it passes through the point (1, 2). The equation of this line can be written by following these steps:
- Take (x1 , y1) = (1, 2) which means x1 = 1 and y1 = 2
- Put m = 3 and (x1 , y1) = (1, 2) in point-slope form
- y − y1 = m(x − x1)
- y − 2 = 3(x − 1)
- Simplify this:
- y – 2 = 3x – 3
- Add 2 on both sides: y – 2 + 2 = 3x − 3 + 2
- y = 3x – 1
Graph:
- Start by plotting the y-intercept (0, -1) on the y-axis.
- Use the slope (m = 3) to find another point:
- Since slope is positive, from point (0, -1), move 3 units up and then 1 unit right. This gives the point (1, 2).
- Draw the line through the points (0, – 1) and (1, 2).
Want to learn more about graphing lines step-by-step? Check out this guide on graphing slope-intercept form.
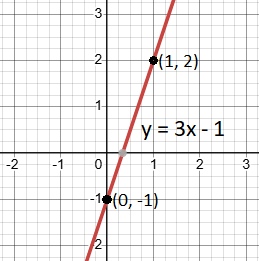
3. Standard Form: Ax + By = C
The standard form of linear equations is written with both variables x and y on the same side, which makes it easy to find intercepts.
- A, B, and C are constants (usually integers).
- This form is commonly used to find the x- and y-intercepts quickly.
Example 3:
Let’s look at the equation 2x + 3y = 6.
- To find the y-intercept, set x = 0:
- 3y = 6 ⇒ y = 2
- So, the y-intercept is (0, 2).
- To find the x-intercept, set y = 0:
- 2x = 6 ⇒ x = 3
- So, the x-intercept is (3,0).
Graph:
- Plot the intercepts (0,2) and (3,0) on the graph.
- Connect the points to draw the line.
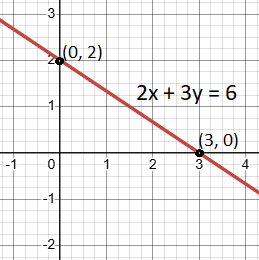
General vs. Standard Form of Linear Equations
General Form: Ax + By + C = 0
- In the general form, the constant C is on the left side of the equation, and the equation is set equal to zero.
- Example: 2x + 3y − 6 = 0
Standard Form: Ax + By = C
- In the standard form, the constant C is on the right side of the equation.
- Example: 2x + 3y = 6.
Key Differences Between General and Standard Form
| Aspect | General Form | Standard Form |
|---|---|---|
| Equation Format | Ax + By + C = 0 | Ax + By = C |
| Constant Position | Constant C is on the same side as Ax and By, set equal to zero. | Constant C is isolated on the right side. |
| Main Focus | Combines all terms on one side of the equation. | Separates the constant, making it easier for graphing. |
| Interception Finding | Harder to find intercepts directly. | Makes finding intercepts easier by setting x = 0 and y = 0 |
| Coefficients | Coefficients can be any real numbers. | Coefficients are typically integers. |
| Usage | More common in algebraic manipulation and systems of equations. | Common for graphing and finding intercepts. |
| Example | 2x + 3y − 6 = 0 | 2x + 3y = 6 |
When to Use Each Form
- Slope-Intercept Form is best when you know the slope and y-intercept and want to graph a line easily.
- Point-Slope Form is helpful when you know one point on the line and the slope.
- Standard Form is useful for finding intercepts and when both x and y variables are important.
Conclusion
In algebra, the three forms of linear equations—slope-intercept, point-slope, and standard—help you represent lines in different ways. Understanding when to use each form and how to switch between them is key to mastering linear equations. Additionally, knowing the difference between general form and standard form allows for more flexibility in solving and graphing equations. Keep practicing these forms, and soon you’ll be able to handle any linear equation with confidence!
By mastering these forms of linear equations, you’ll be well on your way to understanding more complex algebra topics.
Related Posts:
- Introduction. Linear Equation of a line parallel to y-axis
- Linear Equation and graph of a line parallel to x-axis
- What is the Slope of a Line
- How to Calculate the Slope of a Line
- Solved example of finding slope of a line that passes through two given points
- How to Identify Parallel and Perpendicular Lines Using Slopes
- How to derive Linear Equation using Point-Slope Form
- How to easily find X-Intercept and Y-Intercept of a Linear Equation
- Slope-Intercept Form of a Linear equation. A Simple Guide