If you’re just starting to learn linear equation, don’t worry! This guide is designed to make everything clear and simple for you. We’ll explore what a linear equation is, how to solve it, and provide examples to help you understand better. Plus, we’ll include graphs to visually demonstrate how linear equations work, making the concept easy to grasp.
Why is a Linear Equation Called Linear?
The term “linear” is derived from the word “line.” The graph of a linear equation is always a straight-line, no bend or curve. Conversely, a straight-line graph can be represented by a linear equation. Due to this fact, linear equation is also named as general equation of a line.
What is a Linear Equation in Algebra?
A linear equation is a special type of equation. It looks like this:
a x + b y + c = 0 —————– equation (1)
In this equation:
- x and y are variables.
- a, b, and c are numbers (called constants).
- The values of a and b cannot both be zero simultaneously, as this would result in the equation no longer being linear.
As here we represent the variables with letters x and y, so we will call equation (1) as linear equation in x and y.
The power/exponent of variables in Linear equation is always one. That’s way we can say that linear equation is a first-degree equation.
Step-by-Step Examples of Linear Equation and Graph of a line parallel to y-axis
The simplest example of linear equations are the equations used to represent lines parallel to the co-ordinate axis.
x = d ————— Equation (2)
d is a constant
This equation represents a vertical line parallel to the y-axis and intersects the x-axis at point (d, 0). The value of x on this vertical line is always d, regardless of the value of y.
Example 1:
Put d = 1 in equation (2), then the linear equation x = 1 looks like below
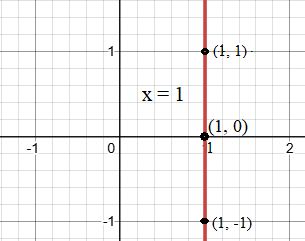
Red vertical line is a graph of equation x = 1. It meets x-axis at point (1, 0). The value of x on this vertical line is always 1, regardless of the value of y.
Example 2:
Solve and graph the linear equation 2x + 3 = 1
Step 1: Isolate the variable.
We need to move the +3 to the other side by subtracting 3 from both sides.
2x + 3 − 3 = 1 − 3
This simplifies to:
2x = – 2
Step 2: Solve for x.
To do this, divide both sides by 2.
![]()
So, x = -1.
Step 3: Plot the graph
To plot the line, do the following:
- On a Cartesian plane, find the point where x = −1.
- Draw a vertical line through (-1, 0), extending it both upwards and downwards.

Red vertical line is a graph of equation 2x + 3 = 1. It meets x-axis at point (-1, 0). The value of x on this vertical line is always -1, regardless of the value of y.
Example 3:
Solve and graph linear equation 3x − 2 = 7
Step 1: Isolate the variable.
Move the -2 to the other side by adding 2 to both sides.
3x − 2 + 2 = 7 + 2
This simplifies to: 3x = 9
Step 2: Solve for x.
Now, solve for x by dividing both sides by 3.
![]()
So, x = 3.
Step 3: Plot the graph

Red vertical line is a graph of equation 3x – 2 = 7. It meets x-axis at point (3, 0). The value of x on this vertical line is always 3, regardless of the value of y.
Example 4:
Solving 4x + 5 = 13
Step 1: Isolate the variable.
Subtract 5 from both sides to move it.
4x + 5 − 5 = 13 − 5
This simplifies to:
4x = 8
Step 2: Solve for x.
Divide both sides by 4 to solve for x.
![]()
So, x = 2.
Step 3: Plot the graph

Red vertical line is a graph of equation 4x + 5 = 13. It meets x-axis at point (2, 0). The value of x on this vertical line is always 2, regardless of the value of y.
Example 5:
Solving 5x − 3 = 2x + 9
Step 1: Move all the x terms to one side
Subtract 2x from both sides.
5x − 2x − 3 = 2x − 2x + 9
5x − 2x − 3 = 9
This simplifies to:
3x − 3 = 9
Step 2: Isolate the variable.
Add 3 to both sides to isolate the x term.
3x − 3 + 3 = 9 + 3
This simplifies to:
3x = 12
Step 3: Solve for x.
Divide both sides by 3 to solve for x.
![]()
So, x = 4.
Step 4: Plot the graph

Red vertical line is a graph of equation 5x – 3 = 2x + 9. It meets x-axis at point (4, 0).The value of x on this vertical line is always 4, regardless of the value of y.
Example 6:
Solving 6x + 8 = 4x + 18
Step 1:
Step 1: Move all the x terms to one side
Subtract 4x from both sides.
6x – 4x +8 = 4x – 4x + 18
This simplifies to:
2x + 8 = 18
Step 2: Isolate the variable.
Subtract 8 from both sides.
2x + 8 – 8 = 18 – 8
This simplifies to:
2x = 10
Step 3: Solve for x.
Divide both sides by 2 to solve for x.
![]()
So, x = 5.
Step 4: Plot the graph

Red vertical line is a graph of equation 6x + 8 = 4x + 18. It meets x-axis at point (5, 0). The value of x on this vertical line is always 5, regardless of the value of y.
Conclusion
This tutorial walks you through solving and graphing various types of linear equations. The red vertical lines in each example indicate where the solutions lie on the x-axis. These steps help you understand linear equations and graphs, making it easier to work with them in algebra problems. Keep practicing with different examples, and soon you’ll master how to solve them confidently.
Related Posts:
- Linear Equation and graph of a line parallel to x-axis
- What is the Slope of a Line
- How to Calculate the Slope of a Line
- How to identify and calculate the undefined slope of a line with easy step-by-step solved example.
- How to Identify Parallel and Perpendicular Lines Using Slopes
- How to derive Linear Equation using Point-Slope Form
- How to easily find X-Intercept and Y-Intercept of a Linear Equation
- Slope-Intercept Form of a Linear equation. A Simple Guide