In this guide, we will explore what the slope of a line is and how to calculate and interpret it using simple examples. The slope tells us how steep a line is and how it changes as we move along the graph. Understanding the slope of a line is essential when working with graphs of linear equations, as it helps us describe how steep a line is and how it moves.
Let’s dive into what slope means and how to find it step-by-step, using examples.
What is the Slope of a Line?
The slope of a line describes how much the line moves up or down as we move left or right. It is a number that tells us how steep the line is. In mathematical terms, the slope is the ratio of the change in the y-values to the change in the x-values between two points on the line.
Formula for Slope
The slope is calculated using the following formula:
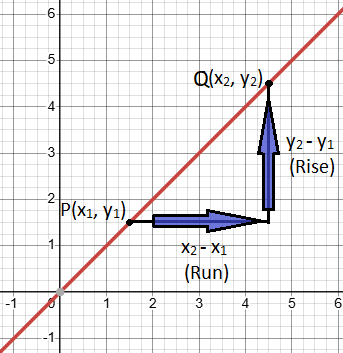
Let ![]() and
and ![]() are two distinct points on a non-vertical line. The slope m is given by:
are two distinct points on a non-vertical line. The slope m is given by:
Slope = m = ![]()
Where:
 represents the vertical change (also called the “rise”). This tells us how much the line goes up or down.
represents the vertical change (also called the “rise”). This tells us how much the line goes up or down. represents the horizontal change (also called the “run”). This tells us how much the line goes left or right.
represents the horizontal change (also called the “run”). This tells us how much the line goes left or right.- Thus, we can say:
- Slope = m =
 ————-(Equation 1)
————-(Equation 1)
- Slope = m =
Key Points to Remember
- The line whose slope is to be calculated should not be vertical, because a vertical line has an undefined slope.
- The points P and Q must be distinct (different from each other).
- It doesn’t matter which point is called P and which one is called Q; reversing the points will reverse both the numerator and denominator in Equation (1), but the ratio stays the same.
Now, let’s explore these key points with examples and graphs.
Step-by-Step Examples
Example 1: Why Vertical Lines Have Undefined Slope
Let’s understand why a vertical line has an undefined slope.
See the following line graph.
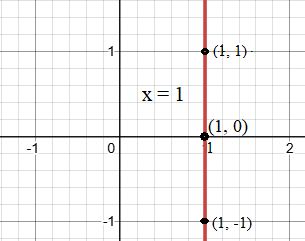
Consider the points (1, 1) and (1, -1) on above red vertical line.
Step 1: Identify the coordinates:
 = (1, 1)
= (1, 1) = (1, -1)
= (1, -1)
Step 2: Find the change in y (vertical change) and x (horizontal change):
- Vertical change (rise):

- Horizontal change (run):

Step 3: Calculate the slope using Equation (1):
Slope = m = ![]() ————-(Equation 1)
————-(Equation 1)
Slope = m = ![]()
Since division by zero is not possible, the slope is undefined.
Conclusion: A vertical line has an undefined slope because the x-values of the points are the same, resulting in a denominator of zero.
Example 2: Importance of Distinct Points
Now let’s see why the points selected must be distinct (different).
See the following line graph.
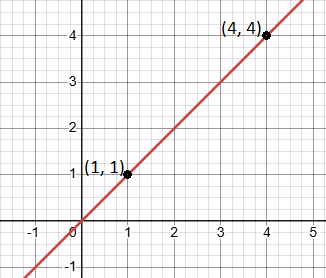
Consider a point P(1, 1) on above red non-vertical line and try to calculate the slope by using the same point for Q.
Step 1: Use the same point for P and Q:
 = (1, 1)
= (1, 1) = (1, 1)
= (1, 1)
Step 2: Find the change in y and x:
- Vertical change (rise):

- Horizontal change (run):

Step 3: Calculate the slope:
![]()
This results in an undefined slope, which means you cannot calculate the slope using the same point twice.
Conclusion: You need two distinct points to calculate the slope of a line.
Example 3: Calculating Slope of a Line Between Two Points
Let’s calculate the slope of a line using two distinct points.
See the following line graph.
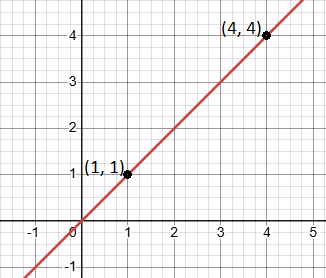
Consider two distinct points (1, 1) and (4, 4) on above red non-vertical line.
Step 1: Identify the coordinates of the points:
 = (1, 1)
= (1, 1) = (4, 4)
= (4, 4)
Step 2: Find the change in y (vertical change) and x (horizontal change):
- Vertical change (rise):

- Horizontal change (run):

Step 3: Calculate the slope using Equation (1):
m = ![]()
Thus, the slope of the line is 1.
Reversing the Points – Does It Change the Slope?
Now let’s see what happens if we switch the points.
Step 1: Reverse the order of the points:
 = (4, 4)
= (4, 4) = (1, 1)
= (1, 1)
Step 2: Find the change in y and x:
- Vertical change (rise):

- Horizontal change (run):

Step 3: Calculate the slope:
m = ![]()
The slope remains 1.
Conclusion: Reversing the points will change the sign of both the numerator and denominator, but the slope remains the same.
Example 4: Using Different Points on the Same Line
Let’s use different points on the same line to confirm the slope stays the same.
Consider the same line graph of example 3.
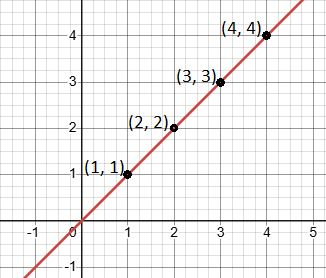
In example 3, we find the slope of a line by considering
![]() = (4, 4) and
= (4, 4) and
![]() = (1, 1).
= (1, 1).
Now, let’s calculate the slope of a line using another pair of distinct points, (2, 2) and (3, 3), which lie on the same line.
Step 1: Identify the coordinates:
 = (2, 2)
= (2, 2) = (3, 3).
= (3, 3).
Step 2: Find the change in y and x:
- Vertical change (rise):

- Horizontal change (run):

Step 3: Calculate the slope:
m = ![]()
The slope is again 1, confirming that the slope is consistent for any two points on the same line.
Conclusion
The slope of a line tells us how steep the line is and whether it goes up or down. It is calculated by finding the vertical change (rise) and dividing it by the horizontal change (run) between two distinct points on the line. The slope remains the same no matter which points you pick on the line, as long as they are distinct. Understanding slope is key to graphing and interpreting linear equations.
This tutorial helps simplify the concept of slope, making it easier for learners to grasp how to calculate and understand the slope of a line!
Related Posts:
- Introduction. Linear Equation of a line parallel to y-axis
- Linear Equation and graph of a line parallel to x-axis
- How to Calculate the Slope of a Line
- How to identify and calculate the undefined slope of a line with easy step-by-step solved example.
- How to Identify Parallel and Perpendicular Lines Using Slopes
- How to derive Linear Equation using Point-Slope Form
- How to easily find X-Intercept and Y-Intercept of a Linear Equation
- Slope-Intercept Form of a Linear equation. A Simple Guide